海风影像馆
zhixinglvren
2022-04-28
目录

排序算法

# 时间复杂度

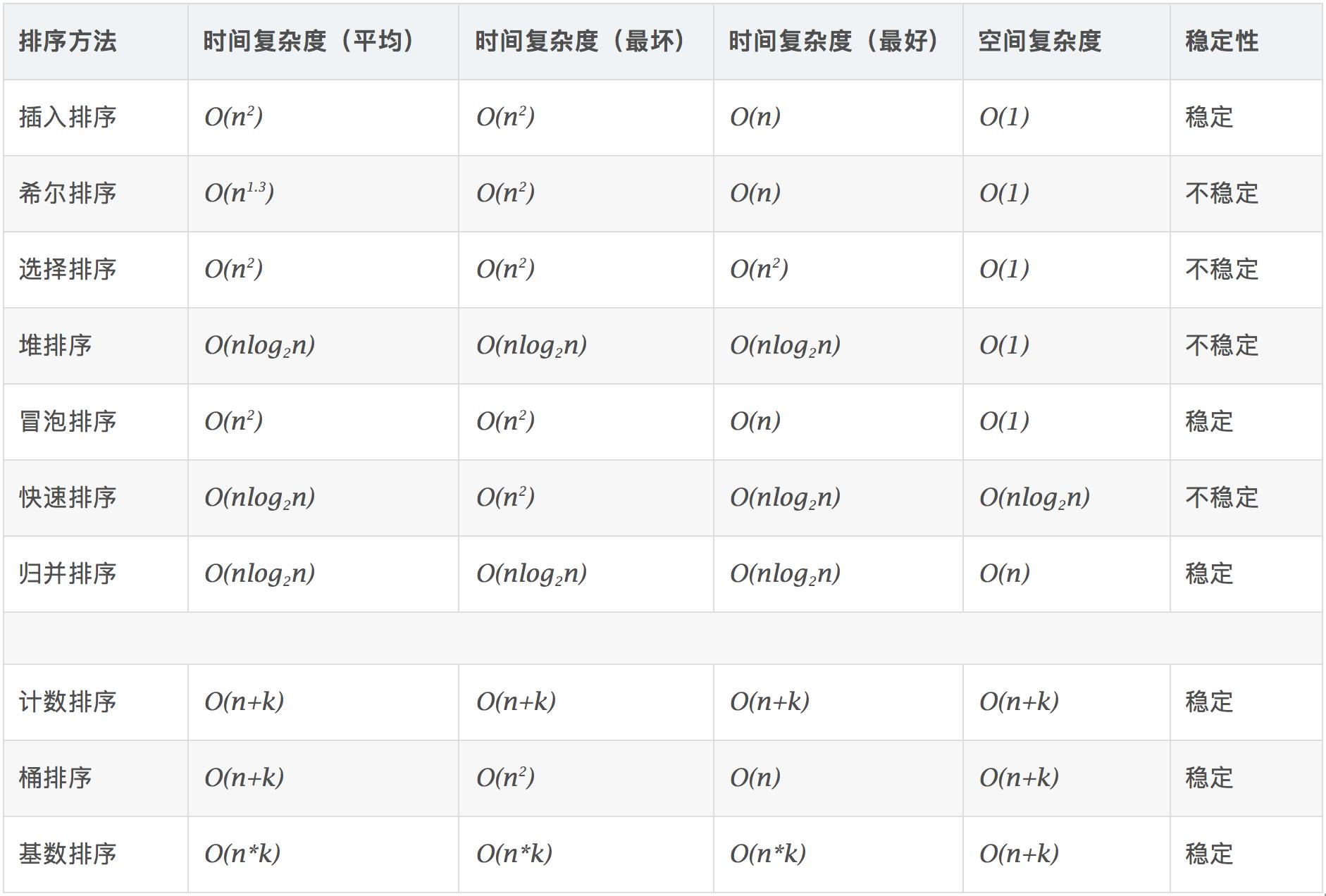
稳定：如果a原本在b前面，而a=b，排序之后a仍然在b的前面。
不稳定：如果a原本在b的前面，而a=b，排序之后 a 可能会出现在 b 的后面。
时间复杂度：对排序数据的总的操作次数。反映当n变化时，操作次数呈现什么规律。
空间复杂度：是指算法在计算机内执行时所需存储空间的度量，它也是数据规模n的函数。

# 七种经典排序

# 1 冒泡排序

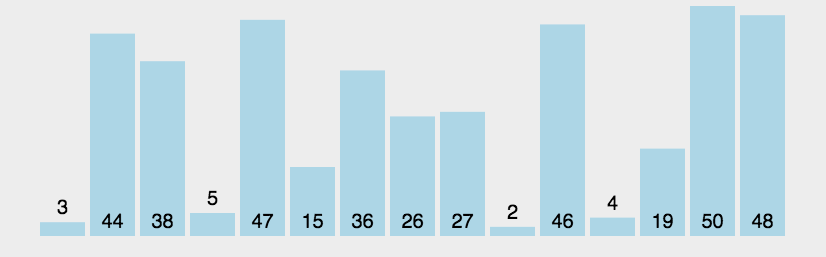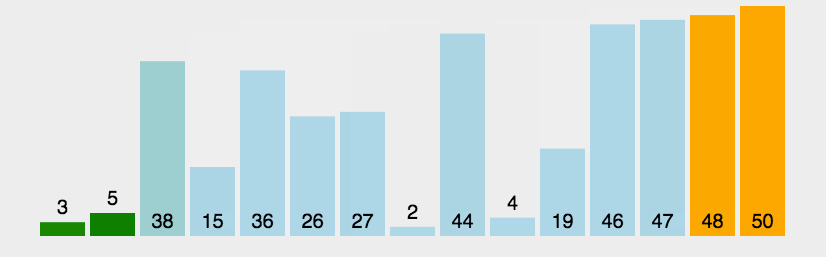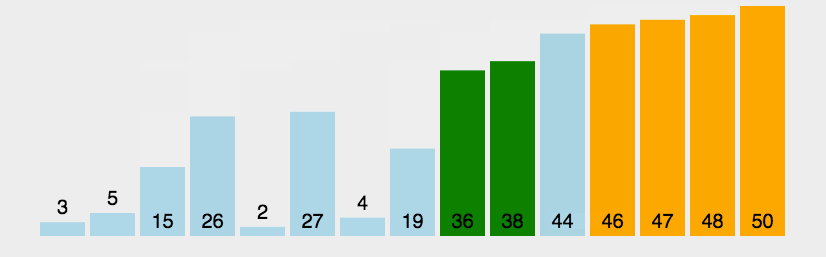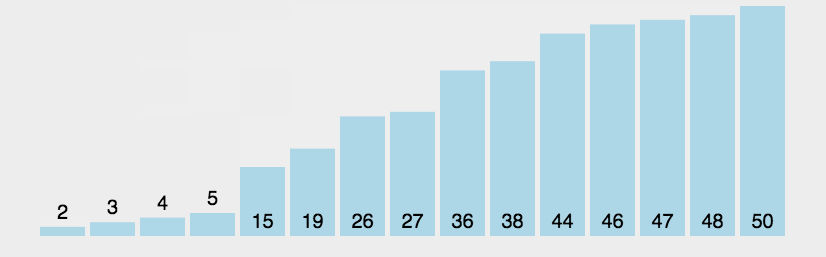
public class BubbleSort {
  public static void main(String[] args) {
    int[] array = {3, 5, 90, 1, 6, 43, 2};
    bubbleSort(array);
  }

  public static void bubbleSort(int[] array) {
    for (int i = 0; i < array.length - 1; i++) {
      for (int j = 0; j < array.length - 1 - i; j++) {
        if (array[j] > array[j + 1]) {
          int tmp = array[j];
          array[j] = array[j + 1];
          array[j + 1] = tmp;
        }
      }
    }
    for (int k : array) {
      System.out.print(k + " ");
    }
  }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

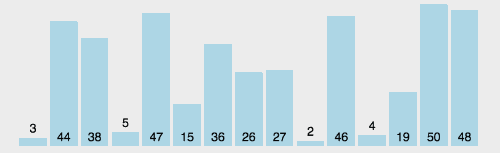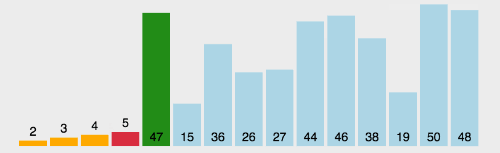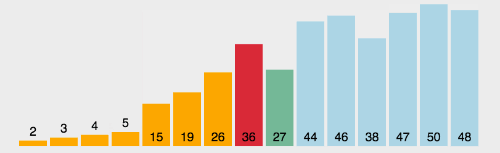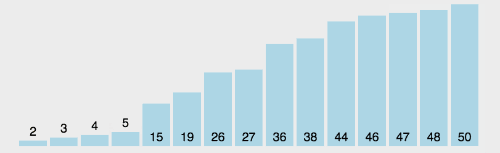
# 2 选择排序

遍历数组，每次找出当次循环中最小的数

  public class SelectSort {
  public static void main(String[] args) {
    int[] array = {3, 50, 90, 1, 6, 43, 2};
    selectSort(array);
  }

  public static void selectSort(int[] array) {
    for (int i = 0; i < array.length - 1; i++) {
      int index = i;
      for (int j = i + 1; j < array.length; j++) {
        if (array[index] > array[j]) {
          index = j;
        }
      }
      if (index != i) {
        int tmp = array[i];
        array[i] = array[index];
        array[index] = tmp;
      }
    }
    for (int k : array) {
      System.out.print(k + " ");
    }
  }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

# 3 快速排序

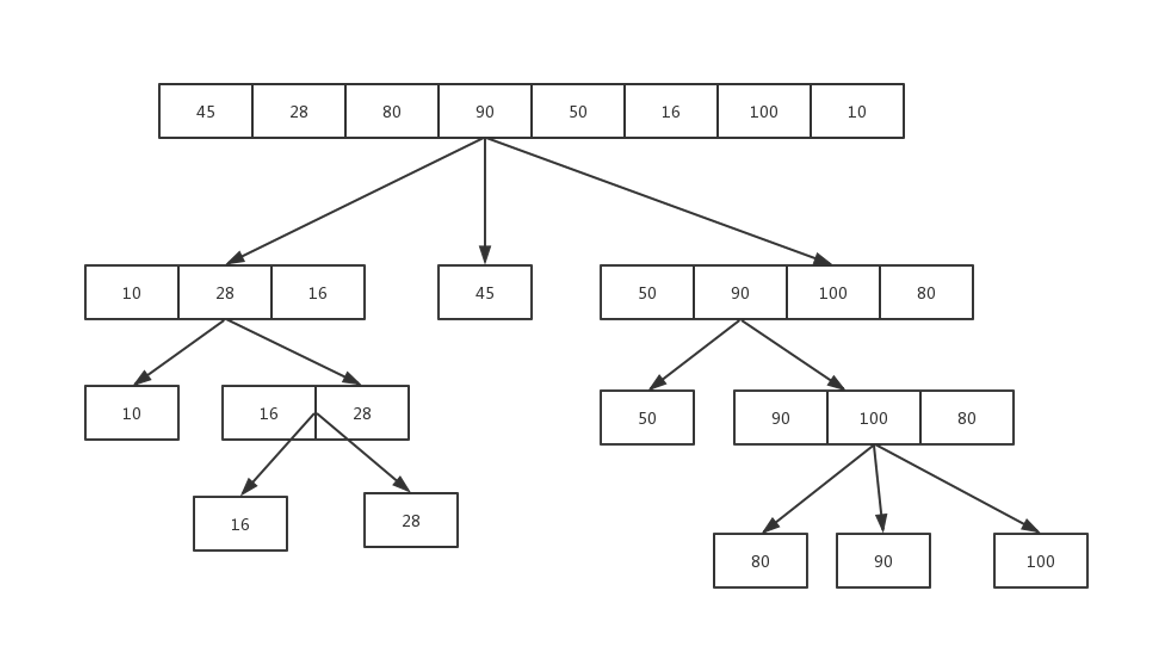
分别从初始序列“6 1 2 7 9 3 4 5 10 8”两端开始“探测”。先从右往左找一个小于6的数，再从左往右找一个大于6的数，然后交换他们。

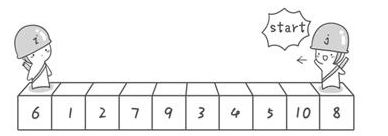
首先哨兵j开始出动。因为此处设置的基准数是最左边的数，所以需要让哨兵j先出动，这一点非常重要（请自己想一想为什么）。哨兵j一步一步地向左挪动（即j–），直到找到一个小于6的数停下来。接下来哨兵i再一步一步向右挪动（即i++），直到找到一个数大于6的数停下来。最后哨兵j停在了数字5面前，哨兵i停在了数字7面前。交换哨兵i和哨兵j所指向的元素的值。

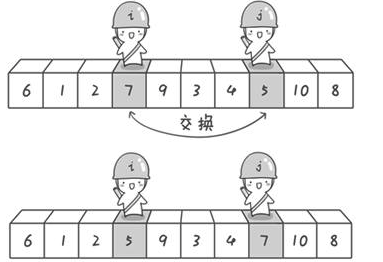
到此，第一次交换结束。接下来开始哨兵j继续向左挪动（再友情提醒，每次必须是哨兵j先出发）。他发现了4（比基准数6要小，满足要求）之后停了下来。哨兵i也继续向右挪动的，他发现了9（比基准数6要大，满足要求）之后停了下来。此时再次进行交换。

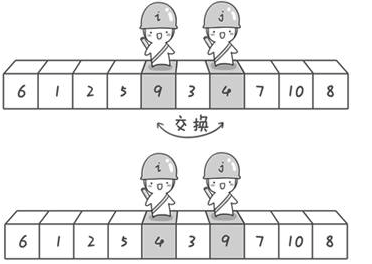
第二次交换结束，“探测”继续。哨兵j继续向左挪动，他发现了3（比基准数6要小，满足要求）之后又停了下来。哨兵i继续向右移动，糟啦！此时哨兵i和哨兵j相遇了，哨兵i和哨兵j都走到3面前。说明此时“探测”结束。我们将基准数6和3进行交换。

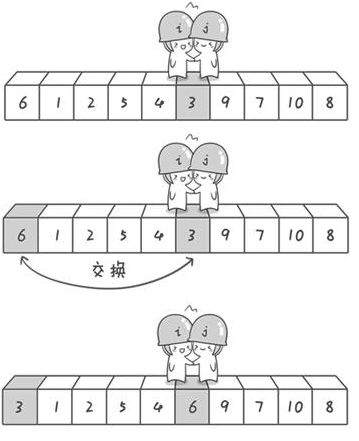
到此第一轮“探测”真正结束。此时以基准数6为分界点，6左边的数都小于等于6，6右边的数都大于等于6。

 public class QuickSort {
  public static void main(String[] args) {
    int[] array = {3, 50, 90, 1, 6, 43, 27};
    quickSort(array, 0, array.length - 1);
    for (int k : array) {
      System.out.print(k + " ");
    }
  }

  public static void quickSort(int[] array, int left, int right) {
    if (left >= right) {
      return;
    }
    int index = left;
    int l = left;
    int r = right;
    while (l < r) {
      while (l < r && array[r] >= array[index]) {
        r--;
      }
      while (l < r && array[l] <= array[index]) {
        l++;
      }
      int temp = array[r];
      array[r] = array[l];
      array[l] = temp;
    }
    int temp = array[index];
    array[index] = array[l];
    array[l] = temp;

    quickSort(array, left, l);
    quickSort(array, l + 1, right);
  }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35

# 4 插入排序

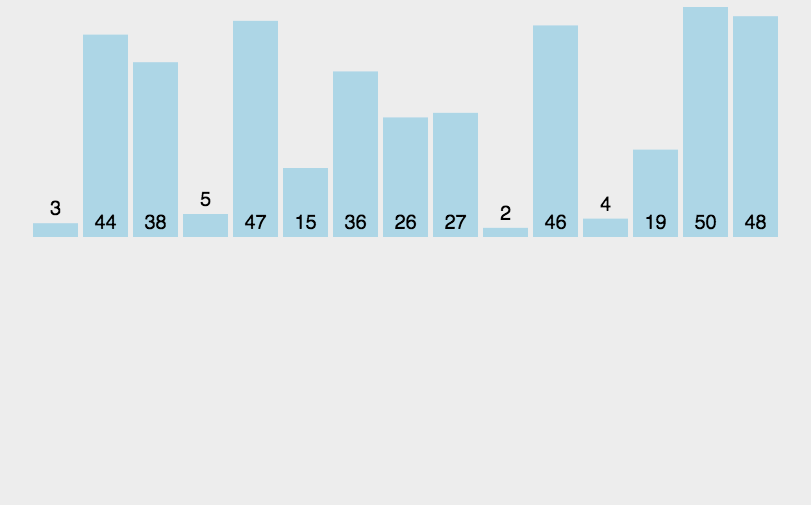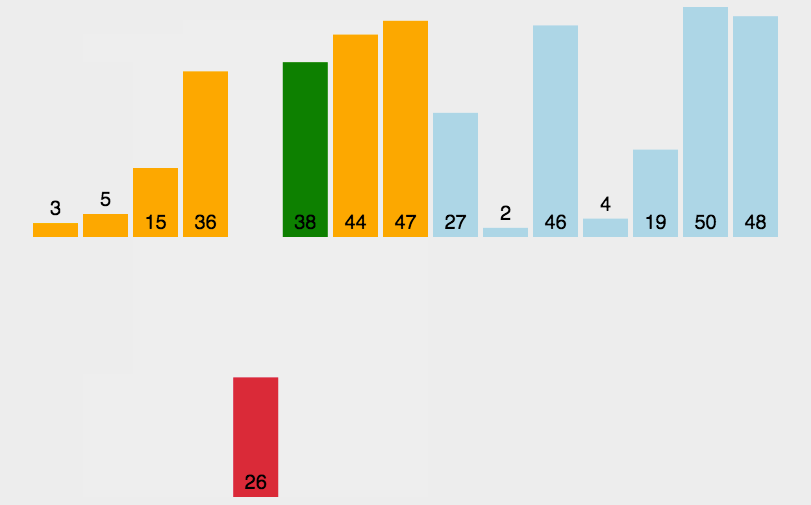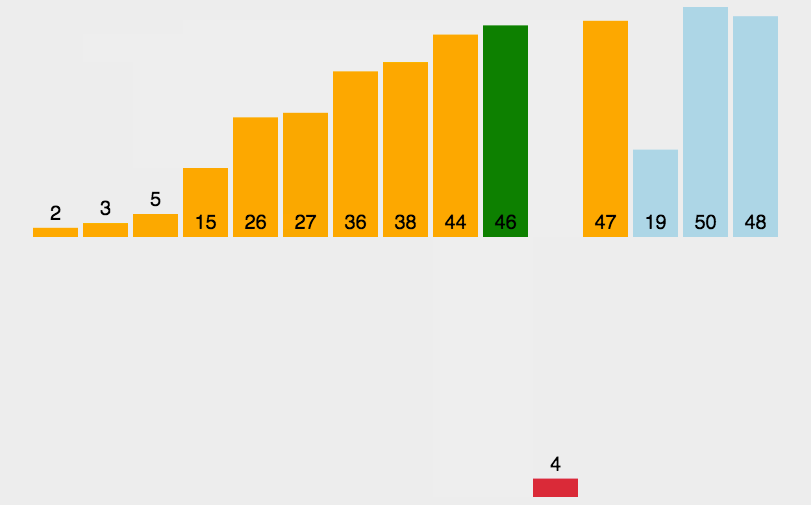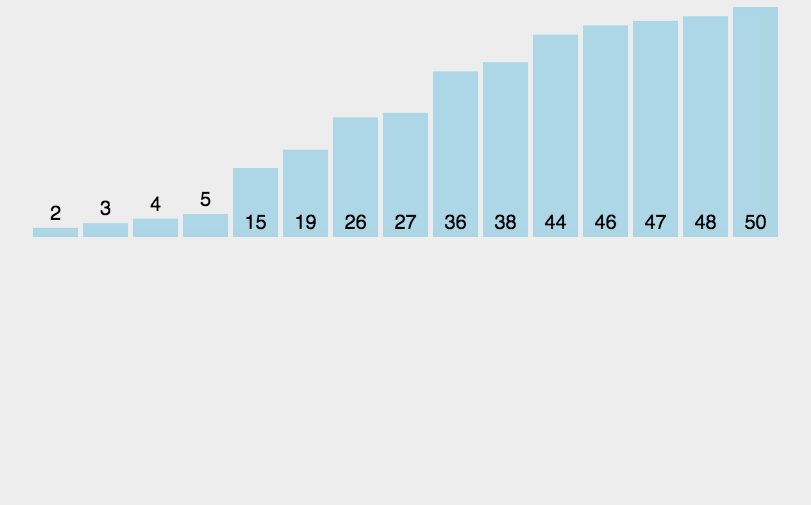
public class InsertSort {
  public static void main(String[] args) {
    int[] array = {4, 8, 6, 1, 2, 3};
    insertSort(array);
    for (int k : array) {
      System.out.print(k + " ");
    }
  }

  public static void insertSort(int[] a) {
    for (int i = 0; i < a.length; i++) {
      for (int j = i; j > 0; j--) {
        if (a[j] < a[j - 1]) {
          int temp = a[j];
          a[j] = a[j - 1];
          a[j - 1] = temp;
        } else {
          break;
        }
      }
    }
  }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

# 5 希尔排序

希尔排序也成为“缩小增量排序”，其基本原理是，现将待排序的数组元素分成多个子序列，使得每个子序列的元素个数相对较少，然后对各个子序列分别进行直接插入排序，待整个待排序列“基本有序”后，最后在对所有元素进行一次直接插入排序。

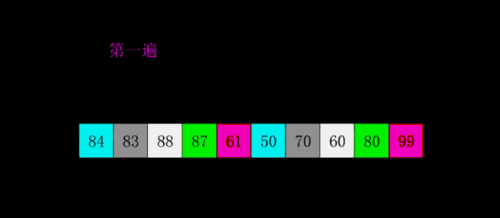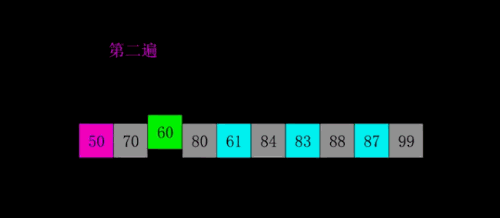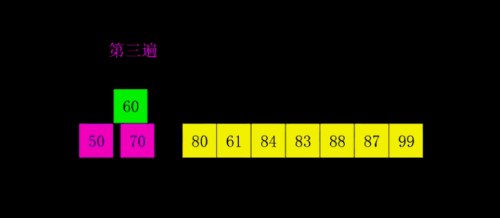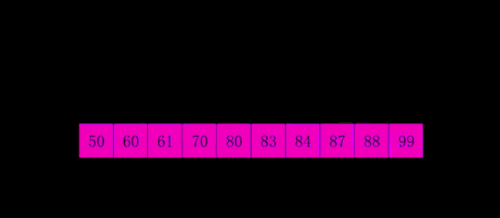
public class ShellSort {
  public static void main(String[] args) {
    int[] data = new int[]{26, 53, 67, 48, 57, 13, 48, 32, 60, 50};
    shellSortSmallToBig(data);
    for (int k : data) {
      System.out.print(k + " ");
    }
  }

  public static void shellSortSmallToBig(int[] data) {
    int j = 0;
    int temp = 0;
    for (int increment = data.length / 2; increment > 0; increment /= 2) {
      for (int i = increment; i < data.length; i++) {
        temp = data[i];
        for (j = i - increment; j >= 0; j -= increment) {
          if (temp < data[j]) {
            data[j + increment] = data[j];
          } else {
            break;
          }
        }
        data[j + increment] = temp;
      }
    }
  }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

# 6 归并排序

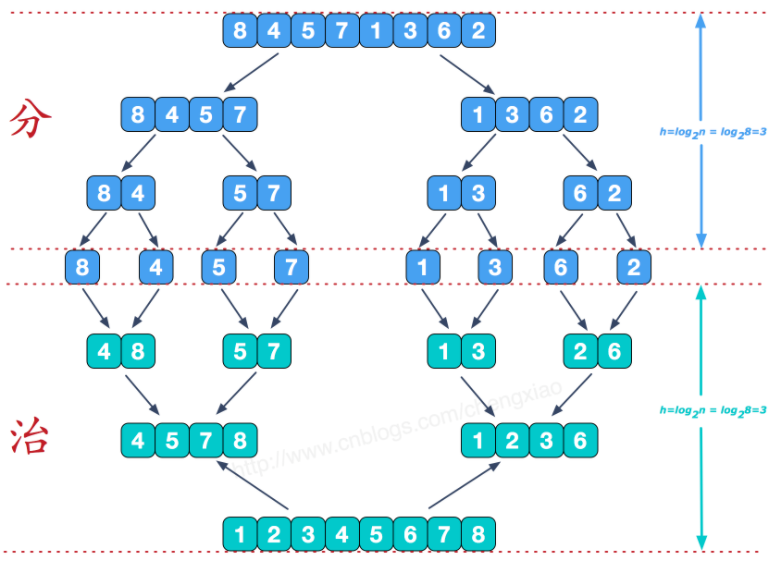
可以看到这种结构很像一棵完全二叉树，本文的归并排序我们采用递归去实现（也可采用迭代的方式去实现）。分阶段可以理解为就是递归拆分子序列的过程，递归深度为log2n。

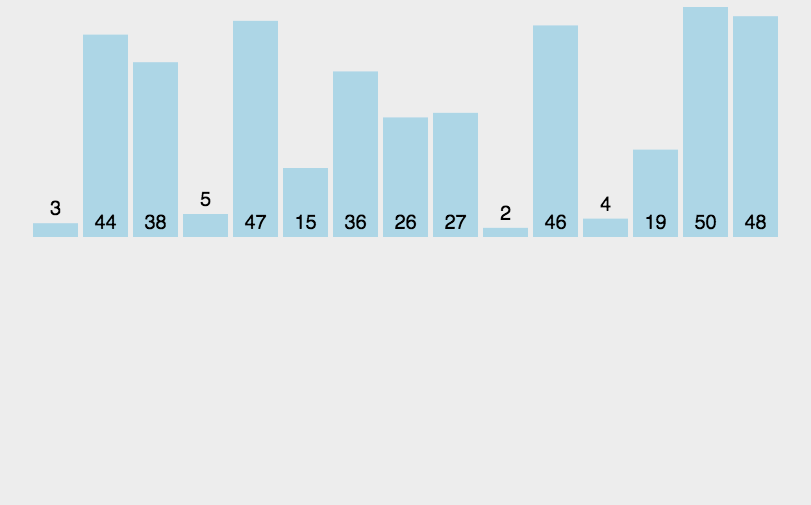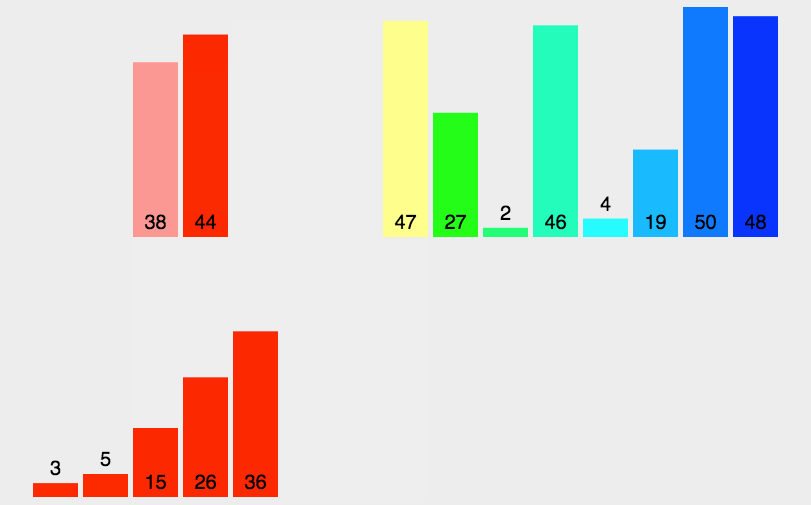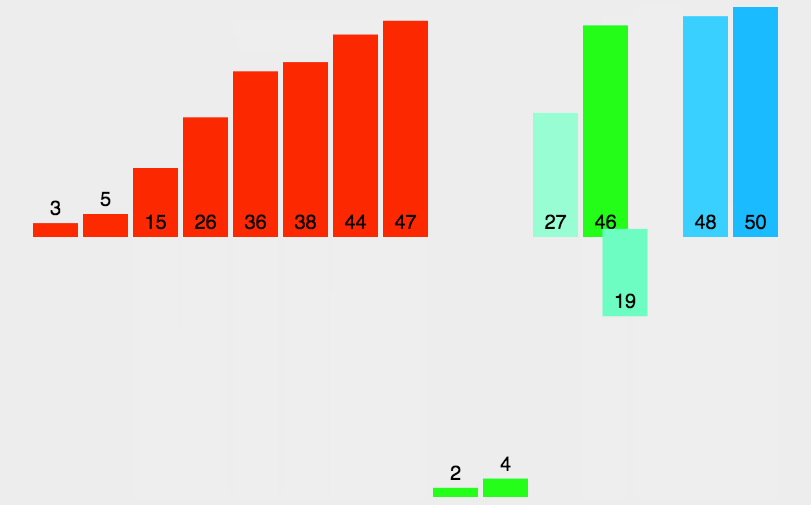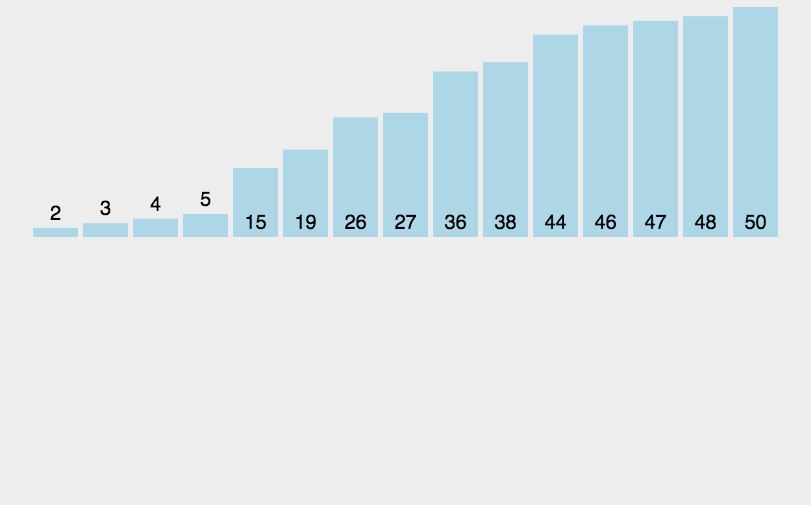
归并排序是稳定排序，它也是一种十分高效的排序，能利用完全二叉树特性的排序一般性能都不会太差。java中Arrays.sort()采用了一种名为TimSort的排序算法，就是归并排序的优化版本。从上文的图中可看出，每次合并操作的平均时间复杂度为O(n)，而完全二叉树的深度为|log2n|。总的平均时间复杂度为O(nlogn)。而且，归并排序的最好，最坏，平均时间复杂度均为O(nlogn)。

public class MergeSort {
  public static void main(String[] args) {
    int[] a = {5, 9, 11, 13, 12, 88, 1, 8, 7};
    System.out.println("初始：" + printArray(a));
    recursive(a, 0, a.length - 1);
    System.out.println("排序：" + printArray(a));
  }

  public static void recursive(int[] array, int left, int right) {

    if (left < right) {
      int mid = (left + right) / 2;
      recursive(array, left, mid);
      recursive(array, mid + 1, right);
      merge(array, left, mid, right);
    }
  }

  public static void merge(int[] array, int left, int middle, int right) {
    int array_l = left;
    int array_r = middle + 1;
    int[] temp = new int[right - left + 1]; //临时数组，存放比较后结果  
    int temp_l = 0; //临时数组左下标  
    while (array_l <= middle && array_r <= right) {
      if (array[array_l] <= array[array_r]) {
        temp[temp_l++] = array[array_l++];
      } else {
        temp[temp_l++] = array[array_r++];
      }
    }
    while (array_l <= middle) {
      temp[temp_l++] = array[array_l++];
    }
    while (array_r <= right) {
      temp[temp_l++] = array[array_r++];
    }
    System.out.println("left:" + left + " middle:" + middle + " right:" + right);
    System.out.println(printArray(temp));
    System.out.println("----------------------------");
    //临时数组数据塞回原数组  
    temp_l = 0;
    while (left <= right) {
      array[left++] = temp[temp_l++];
    }
  }

  public static String printArray(int[] array) {
    StringBuilder sb = new StringBuilder();
    sb.append("【");
    for (int i = 0; i < array.length; i++) {
      sb.append(array[i]);
      if (i != array.length - 1) {
        sb.append(",");
      }
    }
    sb.append("】");
    return sb.toString();
  }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59

# 7 堆排序

什么是堆？

堆是一种非线性结构，可以把堆看作一个数组，也可以被看作一个完全二叉树，通俗来讲堆其实就是利用完全二叉树的结构来维护的一维数组但堆并不一定是完全二叉树

按照堆的特点可以把堆分为大顶堆和小顶堆

大顶堆： 每个结点的值都大于或等于其左右孩子结点的值

小顶堆： 每个结点的值都小于或等于其左右孩子结点的值

使用堆的原因？

如果仅仅是需要得到一个有序的序列，使用排序就可以很快完成，并不需要去组织一个新的数据结构。但是如果我们的需求是对于一个随时会有更新的序列，我要随时知道这个序列的最小值或最大值是什么。显然如果是线性结构，每次插入之后，假设原数组是有序的，那使用二分把它放在正确的位置也未尝不可，但是插入的时候从数组中留出空位就需要O(n)的时间复杂度，删除的时候亦然。

可是如果我们将序列看作是一个集合，我们需要的是这个集合的一个最小值或者最大值，并且，在它被任意划分成为若干个子集的时候，这些子集的最小值或者最大值我们也是知道的，这些子集被不断划分，我们依然知道这些再次被划分出来的子集的最小值或者最大值。而且我们去想办法去保持这样的一个性质，那么这个问题是不是变得非常好解决了呢？那么问题就转换成了一种集合之间的关系，并且是非常明显的一种包含关系，那么最适合于解决这种集合上的关系的数据结构是什么呢？那么就是树，所以就形成了这样的一种树，他的每一个节点都比它的子节点们小或者大。 当我们插入一个新的节点的时候，实际上我们需要去调整的大部分时候只是这棵树上的一条路径，也就是决定它在哪一个集合里面，树上的路径长度相对于这个集合，由于是对数级别的，所以非常可以接受，那么这种数据结构也就应运而生，而这个数据结构为什么叫做堆，那就不知道了。

public class HeapSort {
  public static void main(String[] args) {
    int[] array = {20, 7, 18, 2, 5, 17, 16};
    for (int i = array.length / 2 - 1; i >= 0; i--) {
      adjust(array, i, array.length);
    }
    for (int pos = array.length - 1; pos > 0; pos--) {
      int temp = array[0];
      array[0] = array[pos];
      array[pos] = temp;
      adjust(array, 0, pos);
    }

    for (int k : array) {
      System.out.print(k + " ");
    }
  }

  public static void adjust(int[] a, int index, int len) {
    int endPos = len - 1;
    int left = 2 * index + 1; //左节点  

    int pos = left; //指针指向左节点  
    if (left > endPos) { //左节点超过数组长度  
      return;
    }
    if (left < endPos && a[left + 1] > a[left]) {
      pos = left + 1; //指针指向右节点  
    }
    if (a[index] < a[pos]) {
      int temp = a[index];
      a[index] = a[pos];
      a[pos] = temp;
      adjust(a, pos, len);
    }
  }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
#算法
上次更新: 2022/11/24, 17:59:25
散列表
算法案例

← 算法案例→

最近更新
01
Linux常用指令
11-24
02
GitHub高级搜索技巧
11-24
03
散列表
11-09
更多文章>
Theme by Vdoing | Copyright © 2020-2023 知行旅人 | MIT License | 粤ICP备20036515号-1